How to test randomness?

In this blog I want to show you one way of how to test randomness.

Randomness often appears when programming games. Let’s say you have a class that uses randomness, like a dice. When someone throws a dice it can be in one of six states 1,2,3,4,5 or 6. Thus you might implement the dice using a Java Random like the next example code shows.

import java.util.Random;

public class Dice {

	private Random random = new Random();

	private int number;

	public Dice() {
		throwIt();
	}

	public void throwIt() {
		number = random.nextInt(6) + 1;
	}

	public int getNumber() {
		return number;
	}
}

Can you test that class?

A natural reflex is to say:

“No, you can’t test it, because a test always makes an assumption about the result. Since the result is random you can never make an assumption that will always come true. Thus the test will often fail and somtimes not.”.

But wait for a moment and think about this. The question is what kind of assumption you make. Sure you can not write a test that tests that a specific numer appears when the dice is thrown. But you can test if the randomness fits statistical requirements.

E.g. when you throw the dice 60.000 times. You expect that every number occurs 10.000 times. Well, that would only happen if your random generator would perfectly distribute the values and this might never happen. But again you can assume that each value occurs about 10.000 time +/- 500 times. In other words… you can test that the deviation is less then 5%.

For this statistical distribution you can write a test. All you need is a little helper class that you can use to record the number counts.

import static org.junit.Assert.assertTrue;

class NumberCount {

	private int number;
	private int value = 0;

	public NumberCount(int number) {
		this.number = number;
	}

	public void inc() {
		value++;
	}

	public void assertInBetween(int lower, int upper) {
		assertTrue(number + " - " + value + " > " + lower, value >= lower);
		assertTrue(number + " - " + value + " < " + upper, value <= upper);
	}
}

And the test that makes the assumption that the distribution is within specific bounds.

import java.util.HashMap;
import java.util.Map;

import org.junit.jupiter.api.BeforeEach;
import org.junit.jupiter.api.RepeatedTest;

public class DiceTest {

	private Map<Integer, NumberCount> numberCounts;
	private Dice dice;

	@BeforeEach
	public void setup() {
		dice = new Dice();
		numberCounts = new HashMap<Integer, NumberCount>();
	}

	@RepeatedTest(value = 100)
	public void throwTheDice() {
		int samples = 10_000;
		double deviation = 0.05;

		for (int i = 0; i < 6 * samples; i++) {
			dice.throwIt();
			int number = dice.getNumber();
			NumberCount numberCount = numberCounts.computeIfAbsent(number , NumberCount::new);
			numberCount.inc();
		}

		int lowerBound = (int) Math.floor((double) samples * (1.0 - deviation));
		int upperBound = (int) Math.floor((double) samples * (1.0 + deviation));
		for (NumberCount numberCount : numberCounts.values()) {
			numberCount.assertInBetween(lowerBound, upperBound);
		}
	}

}

Now when you run that test you can ensure that the code you use distributes the dice numbers within the statistical bounds you expect.

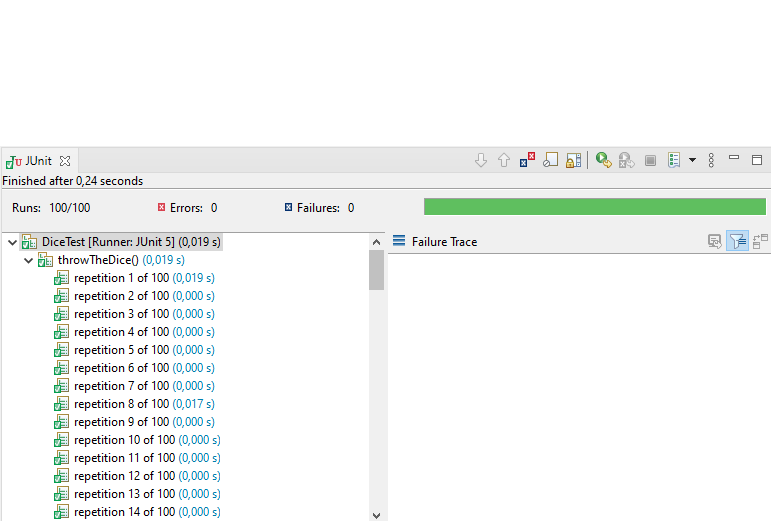
Conclusion

The way to test randomness I showed above can be used sometimes. What I want to show with this blog is that we should never give up to find ways to test the software we write. We should try to push the coverage to 100%, even if we know that this goal might never be reached. But it would be bad if we don’t try.